kyykkä ja koodaamisen iloa. ( Aivan turhaa?)

Posted by: Karli Kund 7 months ago

(2 comments)

Tässä artikkelissa puhutaan kyykästä, koodaamisesta ja teoriasta. Teksti saattaa aiheuttaa pahoinvointia, päänsärkyä, epätoivoa ja ärsyyntymistä. Jos sinulle ilmenee näitä ilmiöitä tämän tekstin luettua, voit laittaa palautetta osoitteeseen roskaposti@roskaposti.fi. Sinua on varoitettu.

Olen harrastanut kyykkää sen 10 vuotta ja aina välillä pyöritellyt päässä eri teorioita, miten karttu etenee tai miten kyykät lentävät, kun niihin osuu. Joskus jopa kentällä keskustelu saattaa mennä erittäin teoriapohjaiseksi ja niistä kai se kipinä tähänkin on lähtenyt. Toki, suurin osasta teorioista ei ole hyötyä käytännössä, koska satunnaismuuttujien ( mitkä ei itselläni ole hallussa) vaikutus lopputulokseen on liian suuri ( kuten 4 tason häirikkö ).

Yhden keskustelun innoittamana tein aikoinaan tämmöisen kuvaajan, missä kuvataan kartun todennäköisyyttä osua kyykkään eri vaiheessa ja eri kartun etäisyydellä kyykästä. Tämä ei kovin helposti auennut ihmisille, vaikka kuinka selitti. Kuvaajassa keltainen alue on tapaukset, missä karttu ei osu kyykkään ja violetilla alueella on tapaukset, missä karttu osuu kyykkään.

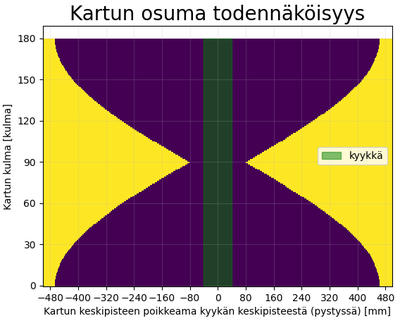
Kuvaajan hyöty jäi pieneksi ja omaksi pieneksi koodaus iloksi. Toki, en itsekään löytänyt mitään sellaista tietoa tästä, mikä hyödyttäisi pelitaktisia päätöksiä. Jätin sen siihen.

Eränä pimeänä ja myrskyisenä yönä sain kuitenkin viestin kaverilta:

Jaa, joku on yrittänyt tulkita kuvaajani. Kyykkätermistö wiki: Lyöväpää kyykässä tarkoittaa, sitä osaa karttua, mikä pyörii kohti kyykkiä. Ei-lyöväpää on osuus mikä pyörii poispäin kyykistä. Olin läbillä kun sain tuon veistin ja pohdin hieman ongelmaa tussitaululla ja laitoin kaverille vastauksen:Ja

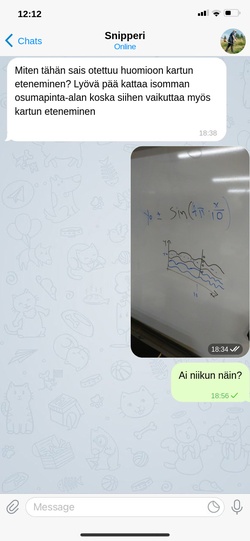
Mutta päässäolevani fysiikkamoottori oli laskenut teorian väärin:

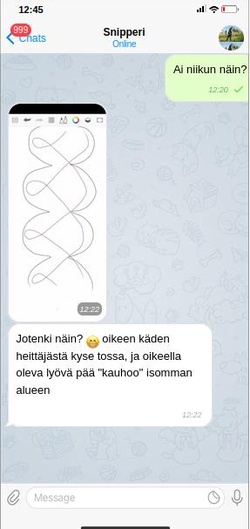
Ajattelin, että kaverini on hieman hupsu, kun tuollaisia käppyröitä piirtelee, mutta ajattelin kuitenkin testa tuota fysiikkasimuloinnilla:

Mein Gott, hän oli oikeassa! Kuvassa siis näkyy kaksi eri karttu, jotka liikkuvat eteenpäin samalla kun ne pyörivät (vasen vastapäivään ja oikea myötäpäivään).  Kartun molempiin päihin on laitettu trackeri (seuraaja), mistä näkee kuljettu rata. Polku tosiaan on eri mitä kuvittelin.

Mutta mieleni ei antanut rauhaa ja huusi vaan ”EI RIITÄ”. Halusin tietää, kuinka paljon suuremman osan lyöväpää kattaa, kun ei-lyöväpää. Tämän on pakko olla joku helppo koodausratkaisu, mistä saan vastauksen sairaan nopee ( jä värikkään!)

Hahmottelin ideaa suihkussa hieman ja tajusin mistä aloittaa. Python, vektori, 2D-rotaatio ja hienoja plotteja!

Seuraavaksi tulee hieman toteutusta, mikä on ei teoreetikolle/koodarille tylsää, joten voi skippaa suoraan kohtaan valmiskuvaaja

if user != koodari || user != teoreetikko:
  GOTO valiskuvaaja

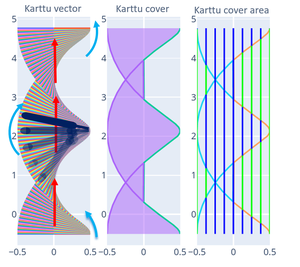
Ensimmäiseksi loin vektorin joka symboli puolikasta karttu [0, 0.85/2]. Tämä vektori sitten pyörisi tietyllä pyörimisnopeudella ja sen nollapiste siirtyisi kappaleen liikenopeuden mukaan. Lasketaan vektorin vaiheet jokaisella aika-askeleella for-loopissa ja vola:

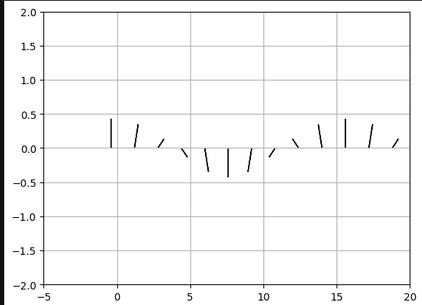
Ei vielä koin vakuuttava, mutta ollaan menossa jonnekin. Piti hieman parantaa koodia, muuttaa skaalausta, lisätä toinen puoli, kiroilla, käydä suihkussa ja nauhoittaa vekotorin pään etenemisen, nii saatiin jo tietää minkä alueen karttu kulkee:

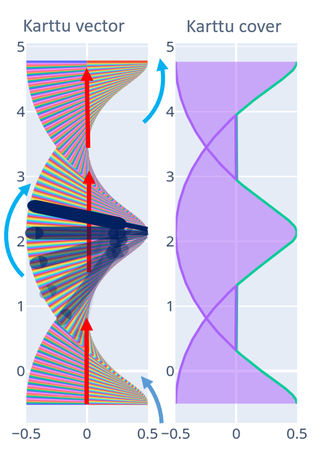
Alkaa jo näyttää. Vasemmalla siis jokaisella aika-askeleella piirretty karttu-vektori ja oikealla sen peittämä alue. Seuraavaksi pitäisi jotenkin laskea sitten peittävän alueen ja ei-peittävän alueen suhde. Se ei heti auennut ja pohdin eri lähestymiä. Sektori-integrointi ois menetelmä mikä ekana tulisi mieleen, mutta aivan turhan hankala. Yksi ongelma myös oli, että kartun molemmat päät kulkevat nollan molemmilla puolilla, mikä hieman vaikeuttaa pinta-alojen laskemista, jos ei halua lähtee jakamaan pinta-aloja erikseen ( enkä halunnut ).Tutkin muita menetelmiä, miten laskea kyseinen pinta-ala. Yksi mikä tuli vastaan oli puolisuunnikassääntö (Trapezoidal rule), mutta se ei oikein miellyttänyt.
Sitten se iski, kesken saunomisen! Kiirehdin tussitaululle ja luonnostelin sen nopeasti. Kämppikset ovat jo tottuneet tähän, eivätkä reagoineet mitenkään. Jaan datajoukuon positiivisiin ja negatiivisiin joukkoihin, jolloin niitä on helpompi pyöritellä! Ja pinta-alasuhteen saadaan piirtämällä viivoja kuvaajaan ja lasken yhteen ne viivat, jotka ovat alueen sisäpuolella. Tässä kuva selvennykseksi:

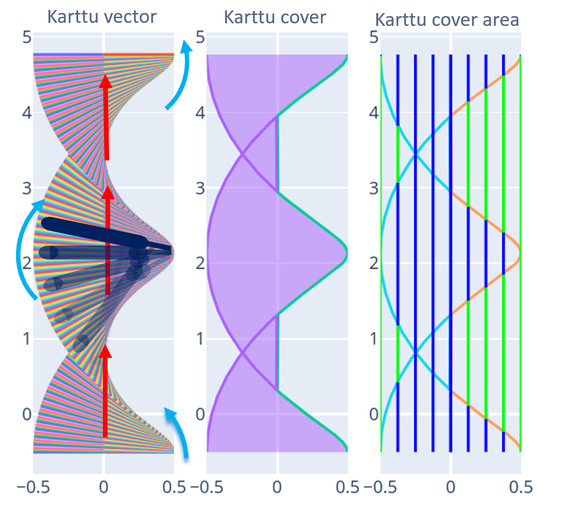
"valmiskuvaaja"

Lasketaan sinisen viivan osuus kokonaispituudesta, nii saadaan tietää suhde. Erittäin helppoa! Kun tiivistää viivojen tiheyden, nii saadaan laskettua lähes täydellinen alueprosenttijakauma:

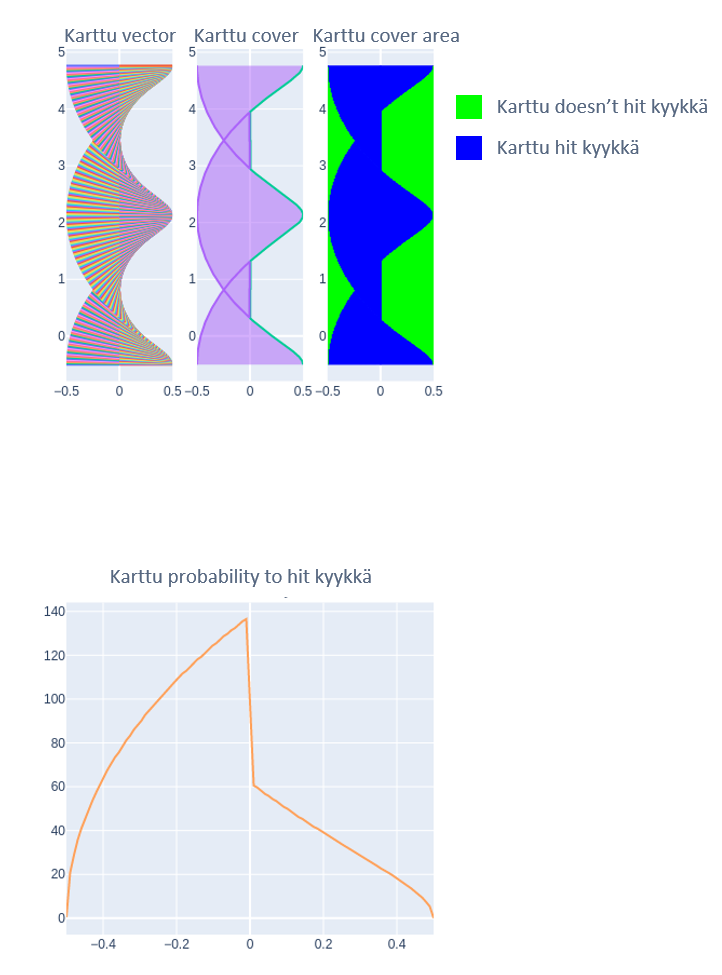
Mahtavaa! Mutta(!), nokkelimmat pokkelimmat huomasivat kuitenkin kuvaajassa jotain outoa: Se menee yli 100%. Aluksi itsekin ihmettelin, sitä ja ajattelin että koodissa on joku virhe ja pyörittelin koodia eri tavalla, kunnes katsoin alkuperäisen simulointivideon uudestaan ja tajusin: karttu käy tuon alueen läpi kahdesti! Kartun lyöväpää pyörähtää siitä läpi ensin ja tämän jälkeen ei-lyöväpää (muuttumassa just lyöväksi pääksi) pyörähtää siitä myös. Eli ei aivan turhaa koodaamista. Kaverikin tykästyi:

Noh, onko tässä sitten käytännössä mitään hyötyä?...Kuten alussa sanoin, monet muut satunnaismuuttujat hallitsevat kartun liikettä sen verran, että tämän ilmiön hyöty jää pieneksi. Tilanne missä tästä olisi hyöty, olisi silloin kun sattuu tähtäämään just tällä yli 100 % alueella ja kartun lyöväpää pomppii kyykästä yli ja ei-lyöväpää vielä pelastaa tilanteen.

Tämmöinen tällä kertaa. Kiitos ja anteeksi. Tuliko tehtyä taas turhaa töitä? Vielä kun joku tästä maksaisi :D

Share on Twitter Share on Facebook

• ← Koivuinen hyllykkö
• Tampere Hacklab pikkujoulut (pre christmas party) ja syyskokous (fall annual meeting) kutsu / invitation 24.11.2023 kello 18.00 →